Sticla lui Klein
Sticla lui Klein a fost descrisă pentru prima dată în 1882 de către matematicianul german Felix Klein. Sticla lui Klein este o suprafata pe care te poti misca din exterior spre interior fara a intersecta vreo margine, o figura geometrica neorientabila, care scoate in evidenta ideea ca interiorul si exteriorul nu sunt neaparat concepte universale. Daca banda lui Moebius este o suprafat bidimensionala marginita, sticla lui Klein nu are margini.
Banda lui Moebius
Din 1930, de când a fost creată, banda lui Moebius a pus probleme mari matematicienilor care vroiau să explice proprietăţile mecanice ale ei. Cea mai mare problemă a fost gasirea unei formule analitice care să definească structura şi tensiunea mecanică in banda lui Moebius, odată ce aceasta este torsionată. Acest lucru a fost însă realizat recent de un grup de doi cercetători de la University College din Londra, Gert van der Heijden şi Eugene Starostin.
Banda lui Moebius a fost descoperită de un matematician german, August Ferdinand Moebius, în anul 1858. Ea a fost popularizată de către artistul olandez M.C. Echer.
Pentru a construi o bandă a lui Moebius, putem începe cu o banda obişnuită de hîrtie. Torsionăm apoi unul dintre capete la 180 de grade, şi îl lipim apoi cu celălalt capăt (vezi figura), formând astfel un cerc neobişnuit. Proprietatea cea mai fascinantă a acestei benzi este că ea pare că are o singură faţă! Astfel, în termeni simpli, am putea spune că şi punctele de pe suprafaţa interioară a benzii, şi punctele de pe suprafaăa exterioară a benzii, fac parte din acelaşi spaţiu bidimensional, din moment ce putem ajunge de la unele de altele, calatorind pe suprafaţa benzii, dar nedepăşind marginile ei. Acest lucru nu ar fi fost posibil cu o bandă circulară obişnuită, netorsionată.
"Ceea de determină forma benzii lui Moebius este energia mecanică inmagazinată în procesul de torsiune", spun ei. Locurile în care banda este torsionată mult au cea mai mare cantitate de energie mecanică înmagazinată. În schimb. locurile din bandă care sunt mai plane şi mai puţin torsionate înmagazinează mai puţină energie. Dacă largimea benzii se modificată, se modifică şi distribuţia de energie din bandă, ceea ce face ca banda lui Moebius să ia o altă formă. Toate aceste procese sunt desigur descrise de ecuaţia recent găsită de cei doi autori.
Aceste cercetări pot apărea exotice, însă Gert van der Heijden şi Eugene Starostin cred că ea poate avea şi aplicaţii practice. Astfel, ele pot fi folosite în predicţia punctelor de stress dintr-o structură asemănătoare benzii lui Moebius, puncte care vor ceda primele la un stress mecanic mai ridicat.
Informaţii preluate de pe site-ul http://www.stiinta.info/.
Ce sunt derivatele şi la ce ne ajută
Una din noţiunile fundamentale ale analizei matematice, chiar a întregii ştiinţe, este cea de derivată. Introducerea noţiunii în matematică este atribuită deopotrivă germanului G. Leibniz (1646 – 1716) şi englezului I. Newton (1642 – 1727). Această noţiune modelează ceea ce s-ar putea numi „viteza de variaţie a unei funcţii”, permite adâncirea studiului local şi global al funcţiilor şi, în acelaşi timp, stă la baza formulării matematice a numeroase legi ale fizicii. De altfel Newton a introdus şi a utilizat conceptul de derivată tocmai în legătură cu studiul legilor mecanicii. Se întâlnesc derivate în studiul vitezei de deplasare a unui mobil, vitezei de variaţie a temperaturii unui corp sau a cantităţii de curent electric, în definiţia densităţii liniare a unei bare şi oriunde interesează rata vreunei schimbări. O altă explicaţie a noţiunii de derivată am găsit-o pe Scientia.ro: „Universul nostru inconjurator este definit de transformari continue, de exemplu, traiectoria unui glont poate fi modelata printr-un set de ecuatii diferentiale. In cazul de fata, transformarea se refera la variatia in timp si spatiu a vitezei obiectului in miscare (deci avem de-a face cu o acceleratie instantanee ,respectiv, convectiva). Cum miscarea se produce intr-un spatiu continuu, interesul nostru este de a lucra cu marimi cat mai mici ca sa surprindem toate aceste variatii fine ale vitezei. Aceste variatii sunt derivate, care sunt de doua tipuri: totale si partiale(daca esti la liceu considera doar primul tip; derivatele totale se refera la variatia unui parametru in raport cu un singur alt parametru, derivatele partiale se refera la variatia in raport cu mai multi parametri, in cazul nostru viteza are derivate partiale in raport cu timpul si cu spatiul). In concluzie, orice fenomen poate fi modelat prin intermediul variatiilor parametrilor, deci predictibilitatea unui fenomen este asigurata prin cunoasterea variatiilor din sistem. O alta interpretare, geometrica, a derivatei este faptul ca derivata intr-un punct al curbei(traiectoriei) este chiar tangenta la acel punct al curbei. Cu cat unghiul tangentei la curba creste cu atat variatiile sunt mai accentuate. O functie care are tangenta de 90 de grade nu mai este derivabila, pentru ca valoarea derivatei este infinita, ceea ce nu se poate.”
Cum se împarte un segment, în mai multe părţi de lungimi egale, doar cu rigla negradată şi compasul
Construcţia geometrică se realizează în mai multe etape.
1. Se trasează (cu rigla negradată) segmentul care trebuie împărţit.
2. Se trasează (cu rigla negradată) o semidreaptă cu originea într-unul din capetele segmentului.
3. Se marchează (cu compasul) pe semidreaptă, de la origine, atâtea segmente de lungimi egale (congruente) câte parţi de lungimi egale trebuie să aibă segmentul.
4. Ultimul punct trasat pe semidreaptă se uneşte (cu rigla negradată) cu celălalt capăt al segmentului.
5. Prin celelalte puncte de pe semidreaptă se duc paralele (cu rigla negradată) la dreapta suport a segmentului construit la punctul 4. Aceste paralele, conform teoremei paralelelor echidistante, intersectează segmentul în puncte care vor împărţi segmentul în părţi de lungimi egale.
Cum se scriu numerele cu cifre romane
Sistemul de numeraţie roman s-a dezvoltat în întervalul 500 î.Hr. – 100 d.Hr. Acest sistem foloseşte cifrele: I(1), V(5), X(10), L(50), C(100), D(500), M(1000). O explicaţie a originii cifrelor romane ar putea fi: C – de la centum (sută); M – de la mille (mie); X – reprezintă două palme cu degetele răsfirate; L – este jumătatea de jos a literei C; V – este jumătatea lui X. În sistemul de numeraţie zecimal se respectă următoarele reguli:
*Când cifrele cu valoare mai mică sunt scrise după cifrele cu valoare mai mare, se adună valorile.
Exemplu: XII = 10 + 1 + 1 = 12
*Când cifrele cu valoare mai mică sunt scrise înaintea celor cu valoare mai mare, se scad valorile.
Exemplu: IV = 5 – 1 = 4
*Cifrele V, L, D nu se scad şi nici nu se pot repeta în acelaşi număr.
*Dacă o cifră cu valoare mai mică se află între două cifre cu valori mai mari, se efectuează întâi scăderea şi apoi adunarea.
Exemplu: XIV = 10 + (5 – 1) = 10 + 4 = 14
*În scrierea unui număr, cifrele I, X, C şi M se pot repeta în poziţii alăturate, dar nu mai mult de trei ori.
Exemplu: LXXX = 50 + 10 + 10 + 10 = 80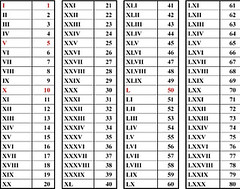
Cum se construieşte bisectoarea unui unghi cu compasul şi rigla ?
Iată răspunsul găsit pe Scientia.ro
Pentru cei care nu ştiu, bisectoarea este o semidreaptă interioară unghiului, cu originea în vârful unghiului şi care formează cu laturile unghiului două unghiuri congruente (de măsuri egale) sau bisectoarea unui unghi este locul geometric al punctelor din interiorul unghiului egal departate de laturile unghiului, reunit cu varful unghiului. Nu se pot măsura unghiuri cu compasul, ci doar trasa cercuri şi arce de cerc. Nu se pot măsura distanţe cu rigla, ci doar trasa linii drepte.
Cu varful compasului in varful unghiului, trasam un arc de cerc care sa intersecteze cele doua laturi ale unghiului, marcand astfel doua segmente congruente (de lungimi egale) care au un punct comun, varful unghiului. Din fiecare din aceste puncte mai trasam cu compasul doua arce care sa se intersecteze in interiorul unghiului. Trasand semidreapta cu originea in varful unghiului si care trece prin punctul de intersectie al celor doua arce de cerc, obtinem bisectoarea unghiului respectiv.
Cum se construieşte mediatoarea unui segment folosind doar o riglă şi un compas ?
Iată răspunsul găsit pe Scientia.ro
Pentru cei care nu ştiu, mediatoarea este perpendiculara dusă pe mijlocul unui segment de dreaptă. Atenţie: rigla nu este gradată, deci nu poate fi folosită pentru a măsura ceva cu ea, ci doar pentru a trasa linii drepte...
Deci mediatoarea unui segment de dreaptă poate fi definită şi ca fiind locul geometric al punctelor egal depărtate de capetele respectivului segment. Modalitatea de construcţie cu rigla şi compasul a mediatoarei este următoarea:
Se construiesc două cercuri de raze egale şi cu centrele în cele două capete ale segmentului. Aceste două cercuri se vor intersecta în două puncte, ca în figura de mai jos. Unind cele două puncte se obţine un segment de dreaptă aparţinând mediatoarei căutate.
Cum se citeste numarul 2.562.553.191.489. 360.000.000?
Iată răspunsul găsit pe Scientia.ro
Pentru denumirea ordinelor de marime (practic a grupurilor de cate trei cifre) se folosesc doua sisteme: scara scurta (SUA si UK) si scara lunga (restul Europei).
Pe scara scurta, puterile lui 10, luate din 3 in 3, sunt mia (10^3), milionul (10^6), bilionul (10^9), trilionul (10^12), cvadrilion (10^15), cvintilion (10^18), sextilion (10^21), septilion (10^24), octilion (10^27).
Pe scara lunga avem mia (10^3), milionul (10^6), miliardul (10^9) , bilion (10^12) - - "o mie de miliarde", biliard (10^15), trilion (10^18), triliard (10^21), quadrilion (10^24), quadriliard (10^27).
Informatiile de mai sus sunt luate de pe pagina wikipedia dedicata numelor numerelor mari.
DEX-ul (penultima editie) introduce multe ambiguitati, prezentand urmatoarele definitii:
BILIÓN, bilioane, s.n. Număr egal cu o mie miliarde sau (în unele țări) cu un miliard.
TRILIÓN, trilioane, s.n. Unitate formată dintr-o mie de miliarde. (10^12)
CVADRILIÓN, cvadrilioane, s.n. O mie de trilioane. (10^15)
CVINTILIÓN, cvintilioane, s.n. O mie de cvadrilioane. (10^18)
SEXTILIÓN s.n. Număr egal cu zece la puterea douăzeci. (10^20)
In concluzie, mergand pe folosirea DEX-ului '98 si folosind pentru bilion definitia conform careia bilionul (ca si trilionul) desemneaza numarul egal cu o mie de miliarde (10^12), numarul din intrebare se va citi astfel:
20 de sextilioane 562 de cvintilioane 553 de cvadrilioane 191 de trilioane 489 de miliarde 360 de milioane.
In opinia noastra DEX-ul '98 nu este adaptat terminologiei internationale folosite in acest domeniu. Cf. scarii lungi pomenite anterior, numarul s-ar citi astfel:
2 triliarde 562 de trilioane 553 de biliarde 191 de bilioane 489 de miliarde 360 de milioane(cu precizarea ca termenii folositi nu exista cu toti in editia mentionata anterior a DEX).
I. Newton, geniul distrat
Pentru unii autori, Newton este, cronologic, al doilea geniu matematic al omenirii, fiind precedat de Arhimede (grec) şi urmat de Gauss (german). Englezul Newton era mereu cu capul în nori, preocupat de problemele sale matematice. Sunt multe anecdote care-l au ca personaj pe cel căruia îi datorăm cunoaşterea şi performanţele tehnice de azi. De exemplu, se spune că Newton, care era celibatar, a vrut să-şi fiarbă un ou fără să-şi întrerupă lucrul. Îşi luă ceasul său de precizie ca să se uite la el şi să vadă când au trecut cele trei minute pentru fierbere. Era însă preocupat mult de tema pe care o trata. Când, într-un târziu, şi-a amintit de oul pus la fiert, a constat cu uimire că a pus ceasul la fiert, iar oul îl ţinea în mână pentru a citi minutele. Altădată, Newton a invitat un bun prieten al său la masă. Acesta vine la ora fixată şi, ca să nu-l deranjeze pe Newton de la lucru, se duce direct în sufragerie, aşteptând ca ilustrul său prieten să termine lucrul şi să vină la masă. Dar Newton nu mai ieşea din biroul său de lucru. Atunci prietenul, răzbit de foame, se aşeză la masă, pe care era un pui fript sub un clopot, mâncă o jumătate de pui şi plecă fără să-l avertizeze pe Newton. Mult mai târziu l-a răzbit foamea şi pe Newton. Savantul uitase complet de invitaţia pe care o adresase prietenului său. Newton vine în sufragerie, vede că lipseşte o jumatate de pui şi-şi spuse: „Uite ce distrat sunt; am mâncat şi am uitat”. Şi se întoarce la lucru.
Curiozităţi aritmetice ale numerelor
1 + 2 + 3 + … + 10 = 55;
1 + 2 + 3 + … + 100 = 5.050;
1 + 2 + 3 + … + 1.000 = 500.500;
……………
1*1 = 1;
11*11 = 121;
111*111 = 12.321;
1.111*1.111 = 1.234.321;
11.111*11.111 = 123.454.321;
…………..
1*9 + 2 = 11;
12*9 + 3 = 111;
123*9 + 4 = 1.111;
1.234*9 + 5 = 11.111;
12.345*9 + 6 = 111.111;
123.456*9 + 7 = 1.111.111;
………….

Cuadratura cercului
În ‘cuadratura cercului’, aşa cum este numită prescurtat, este vorba de un ‘cuadrat’, adică pătrat, şi de un cerc. Enunţul complet al acestei vestite probleme nerezolvabile aşa cum s-a propus este următorul: “Se dă un cerc; să se construiască numai cu linia (rigla) şi compasul pătratul care închide aceeaşi arie ca şi cercul”. Mai întâi de toate, din acest enunţ, se vede că trebuie să construim numai cu rigla şi compasul un pătrat care să închidă între laturile sale exact aceeaşi arie ca şi cercul, sau, altfel spus, pătratul să fie echivalent cu cercul. Pătratul trebuie să aibă exact aceeaşi arie ca şi cercul şi nu cu aproximaţie. Trebuie deci fie să calculăm aria cercului de rază dată şi să aflăm apoi latura pătratului echivalent, fie să construim (grafic), când ni se dă cercul, pătratul echivalent. Problema a fost pusă în acest mod la greci acum aproximativ 2.400 de ani, cu mult înainte de Euclid, şi a preocupat atât pe matematicieni, cât şi pe nespecialişti. Era pusă astfel problema, adică să se realizeze numai cu rigla şi compasul, fiindcă în epoca de aur grecească a matematicilor (600 – 200 î. Hr.) se considera că numai aceasta era o rezolvare pur geometrică. Problema calculării pătratului echivalent cercului este şi mai veche şi o întâlnim la egipteni, într-un papirus scris în jurul anului 1800 î. Hr. Cuadratura cercului are o vechime de aproximativ 3.800 de ani!
Legat de cuadratura cercului este şi rectificarea (aflarea lungimii) cercului, adică determinarea prin calcul sau construirea unui segment de aceeaşi lungime ca şi cercul. Iar aici apare o constantă celebră, notată π (pi) şi numită constanta cercului. Pentru cei care au petrecut orele de matematică pe terenul de sport sau cu oile, precum Gigi Becali, trebuie amintit că un cerc are o măsură şi o lungime. Măsura este exprimată în grade sexagesimale (sau în radiani), iar un cerc are măsura de 3600 sau 2π rad. Lungimea cercului este exprimată în metri, iar un cerc are lungimea de 2πr m, unde r reprezintă raza cercului. Revenind la constanta cercului (π), aceasta apare în felul următor: la orice cerc, raportul dintre lungimea cercului şi diametrul său este constant şi egal tocmai cu numărul π. Acest număr celebru are o istorie mai mult decât interesantă. De exemplu, egiptenii considerau π ≅ 3,1604, mai mare decât valoarea reală a lui π cu aproximativ 0,0188. Arhimede a considerat 3,01408<π<3,1428. Cuadratura cercului, aşa cum a fost pusă iniţial de greci, nu-i realizabilă şi s-a demonstrat că nu poate fi rezolvată, după cum se va vedea în continuare. La sfârşitul Evului Mediu şi în timpul Renaşterii, cuadratura cercului prezenta un aspect mistic. Se presupunea că avea urmări tainice, necunoscute, ca un fel de piatră filozofală abstractă. Cine o va rezolva, va putea înţelege o mulţime de fapte supranaturale.
La sfârşitul secolului al XVI-lea, Ludolph van Ceulen şi-a propus să determine pe π (constanta cercului) în limite mai strânse decât o făcuse Arhimede cu 18 secole mai înainte. Astfel, olandezul van Ceulen a stabilit valoarea lui π (prin metoda perimetrelor) cu 34 de zecimale exacte. Cam în aceeaşi perioadă, Adriaan Anthonitz a stabilit că π este cuprins între 3 întregi şi 15/106 şi 3 întregi şi 17/120. De aici a scos o valoare medie pentru π, 355/113, cunoscută după aceea sub numele de ‘aproximaţia lui Metius’. Începând cu François Viète se trece de la metode geometrice de calcul pentru π la metode analitice. Până în secolul XX, mulţi matematicieni s-au ocupat de calculul valorii lui π, obţinând rezultate din ce în ce mai exacte. În ziua de azi, π se poate calcula cu oricâte zecimale exacte se doreşte (π = 3,1415926535 …). Revenind la cuadratura cercului, germanul Ferdinand Lindemann a demonstrat în 1882 că problema nu este rezolvabilă cu rigla şi compasul într-un număr finit de paşi. Iar aceasta pentru că π este un număr transcendent, nu un număr algebric (un număr este algebric dacă este rădăcină a unei ecuaţii cu coeficienţi raţionali şi transcendent în caz contrar). Adică este imposibil să construim cu rigla şi compasul un pătrat al cărui arie să fie egală cu cea a unui cerc dat.













Niciun comentariu:
Trimiteți un comentariu